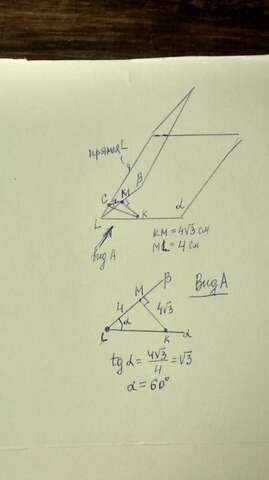
Обозначим
с = ? длина наклонной от точки Р до плоскости β
а = 6см - проекция наклонной на плоскость β
h = ? - расстояние от точки Р до плоскости
α = 30° - угол между наклонной и плоскостью β (угол между наклонной с и её проекцией а)
Угол между h и а равен 90°, поэтому а, с и h образуют прямоугольный треугольник с острым углом α= 30°
Гипотенуза с = а/cos30° = 6 ^ 0.5√3 = 4√3 (cм)
Катет h, лежащий против угла в 30°, равен 0,5 гипотенузы с
h = 0.5 c = 0.5 · 4√3 = 2√3(см)
Ответ: длина наклонной равна 4√3см; расстояние от точки до плоскости равно 2√3см