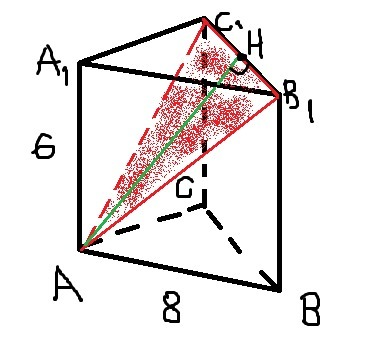
Дано:
ABCA1B1C1 - правильная треугольная призvf
AB=8см
AA1=6см
Найти S сеч. -?
Решение:
1)Построим сечение:
(B1C1 - (это сторона верхнего основания), А - ( это противолежащая вершина))
Проводим B1A в (AA1B1B)
Проводим АС1 в (АА1С1С)
В1С1А - искомое сечение, равнобедренный треугольник, т.к B1A =АС1
2)по теореме Пифагора из треугольника AA1B1 - прямоугольного:
B1A^2 = AA1^2+A1B1^2
отсюда:
B1A^2= 36+64=100
B1A=10
3) по формуле:
S=√p(p-a)(p-b)(p-c)
S=√14*4*4*6=8√21
Ответ:8√21
или можно найти высоту АН сечения, она равна 2√21
и потом находим S=a*h/2
S=8*2√21/2=8√21