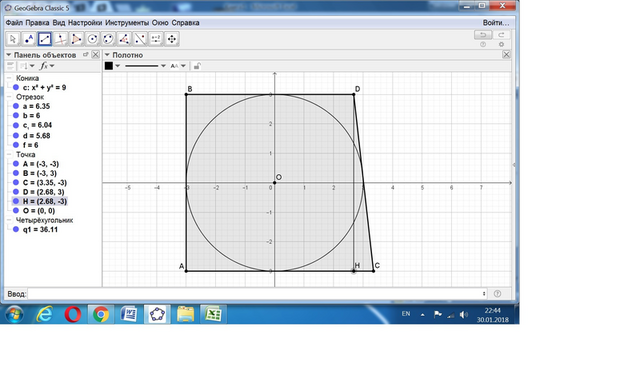
По свойству касательных к окружности обозначим отрезки от вершины до точки касания, равными 4х и 5х.
Проведём высоту трапеции из вершины верхнего основания на нижнее.
Получим прямоугольный треугольник с катетами, равными 6 и (5х + 4х = х).
Гипотенуза (это наклонная боковая сторона трапеции) равна 5х + 4х = 9х.
По Пифагору (9х)² = 6² + х².
81х² = 36 + х².
80х² = 36.
20х² = 9.
х = √(9/20) = 3/(2√5) = 3√5/10.
Средняя линия Lср трапеции равна 3 + ((4х + 5х)/2) = 3 + (9х/2).
Подставим значение х:
Lср = 3 + (27√5/20) ≈ 6,018692.
Тогда искомая площадь S трапеции равна:
S = 6*Lср = 6*(3 + (27√5/20)) =
18 + (81√5/10) ≈ 36,11215 кв.ед.