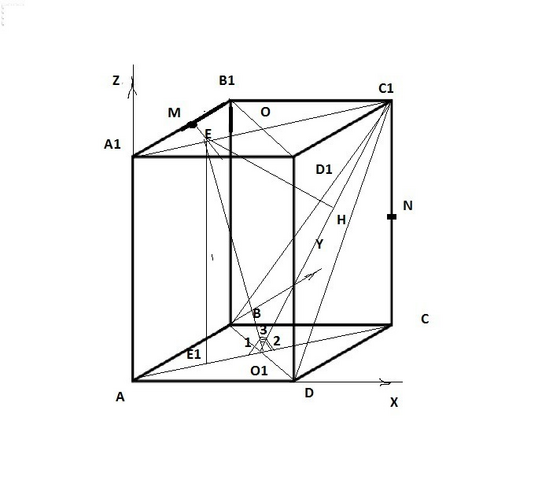
Расстояние от M до плоскости BDC1 равно ЕH,
которое найду из прямоугольного ΔEO1H.
EH=O1E*sin<3<br><3=180-(<1+<2)<br>O1E из ΔE1O1E : O1E^2=(1/2)^2+2^2=17/4; O1E=√17/2
cos<1=O1E1/O1E=1/2:√17/2=1/√17<br>из ΔС1O1C найду cos<2<br>C1O1^2=CC1^2+O1C^2=4+1=5;C1O1=√5
cos<2=O1C/C1O1=1/√5<br>cos<3=cos(180-(<1+<2))=-cos(<1+<2)=-(cos<1*cos<2-sin<1*sin<2))<br>sin<1=√(1-1/17)=4/√17; sin<2=√(1-1/5)=2/√5<br>cos<3=-(1/√17*1/√5-4/√17*2√5)=7/√85<br>sin<3=√(1-49/85)=6/√85<br>EH=√17/2*6/√85=3/√5
Ответ: расстояние от точки М до плоскости BDC1 равно 3/√5