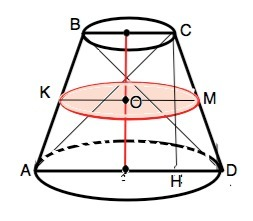
Осевое сечение усеченного конуса - равнобедренная трапеция АВСD с равными диагоналями. .
Взаимно перпендикулярные равные диагонали образуют с основаниями прямоугольные равнобедренные треугольники. Сумма высот этих треугольников=сумме их медиан=полусумме оснований. Отсюда: Если диагонали равнобедренной трапеции перпендикулярны, то её высота равна средней линии трапеции, т.е. полусумме оснований.
Сечение конуса, проведенное параллельно основанию, – круг.
Диаметр КМ сечения, проведенного через середину высоты осевого сечения параллельно основанию, равен средней линии такой трапеции, т.е. Н. Тогда радиус ОМ равен Н/2, а площадь
S=π•(H/2)²=π•Н²/4