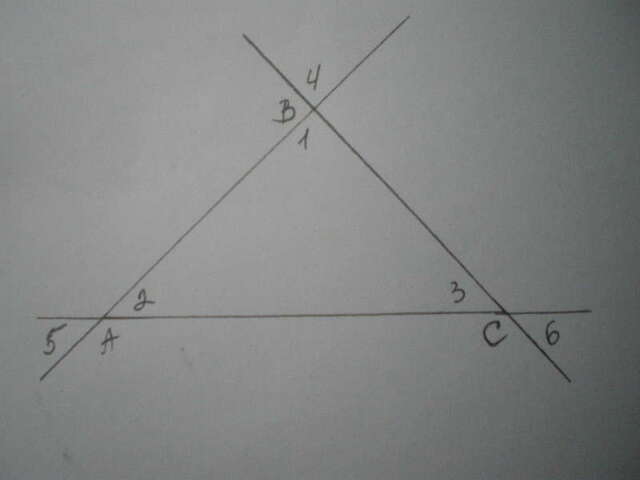
Всего у треугольника шесть внешних углов, по два при каждой вершине.
Углы каждой пары равны между собой (как вертикальные):
∠1=∠4, ∠2=∠5, ∠3=∠6.
По теореме, внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Поэтому: ∠1=∠А+∠С, ∠2=∠С+∠В, ∠3=∠В+∠А.
Отсюда сумма внешних углов треугольника, взятых по одному при каждой вершине, равна
∠1+∠2+∠3=∠А+∠С+∠А+∠В+∠В+∠С=2(∠А+∠В+∠С).
Так как сумма углов треугольника равна 180º, то ∠А+∠В+∠С=180º. Значит, ∠1+∠2+∠3=2∙180º=360º.