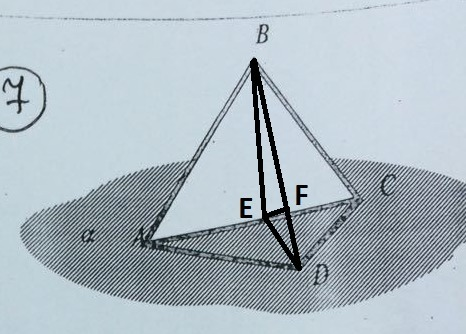
В треугольниках ABC и ABD проведём высоты. Обе они делят общую сторону AC пополам, т.к. треугольники равнобедренные (BE и DE - медианы).
AE = EC = AC/2 = a/2.
1) ΔADC:
Пусть AD = CD = b. Тогда по т. Пифагора
a² = b²+b²
a² = 2b²
b = a/(√2).
Также ∠DAC = ∠DCA = 45°
∠ADE = 1/2·∠ADC = 45°, т.к. DE - высота, биссектриса и медиана.
2) ΔADE:
∠AED = 90°, ∠EAD = ∠EDA = 45°, следовательно, ΔADE - равнобедренный.
AE = DE = a/2.
3) ΔABE:
По т.Пифагора
BE = √(AB²-AE²) = √(a²-a²/4) = (a√3)/2
4) ΔBED:
По т.Пифагора
BD = √(BE²+DE²) = √(3a²/4+a²/4) = a
EF - расстояние от AC до BD и одновременно высота, опущенная на гипотенузу прямоугольного треугольника BED
EF = (BE·ED)/BD = ((a√3)/2·a/2)/a = (a√3)/4