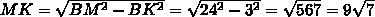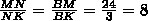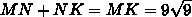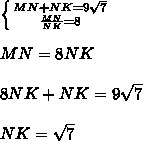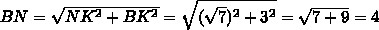На середине отрезке АВ возьмём точку О и проведём окружность радиусом АО=ОВ. Тогда наша окружность пройдёт через точки М и N, т.к. по условию углы ∠AMB = ∠ANB = 90°.Лучи BM и BN делят угол ABC на три равные части меньше 45°. Отсюда, равны углы ∠ABN = ∠MBC, т.к. содержат в себе по две равные доли угла АВС.Углы ∠BAN и ∠BMN опираются на одну и ту же дугу ∪BN, следовательно, эти углы равны: ∠BAN = ∠BMN. Значит, треугольники ΔBAN и ΔBMK подобны по двум углам, и угол ∠BKM = 90°, как ∠ANB.Найдём МК по теореме Пифагора:
Рассмотрим треугольник ΔMBK. Биссектриса треугольника BN делит сторону на отрезки, пропорциональные прилежащим сторонам:
С другой стороны, ранее мы нашли, что
Составляем систему уравнений и решаем:
По теореме Пифагора находим BN: