ДАНО
Y = 4*㏑x - x²/2
ИССЛЕДОВАНИЕ
1.Область
определения D(x) X>0 - Х∈(0;+∞)
- непрерывная.
Вертикальная асимптота - X = 0.
Горизонтальной асимптоты - нет.
Наклонной асимптоты - нет.
2.
Пересечение с осью Х. Y=0 при х1 ≈ 1.1956, x2 = 2.9348 .
Положительна
- между корнями, отрицательна - X∈(0;x1)∪(x2;+∞).
3. Пересечение
с осью У - нет. У(0) = 0.
4. Поведение
на бесконечности.limY(0) = - ∞, limY(+∞) = -∞
5.
Исследование на чётность.Y(-x) ≠ - Y(x), Y(-x) ≠Y(x)
Функция ни четная ни нечетная.
6.
Производная функции.Y'(x)= - x + 4/x = 0.
Максимум
Ymax(2)= -2+ 4*ln(2)
7.
Интервалы возрастания и убывания.
Возрастает
- Х∈(0;2],
убывает = Х∈(2;+∞).
8.
Вторая производная - Y"(x) = 4 - x² =0.
Корней - нет, точек перегиба - нет.
9.
Выпуклая “горка» Х∈(0;+∞).
10.
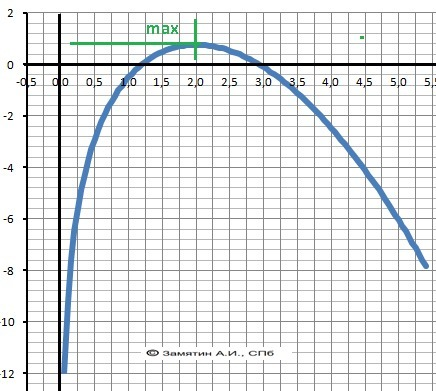
График в приложении.