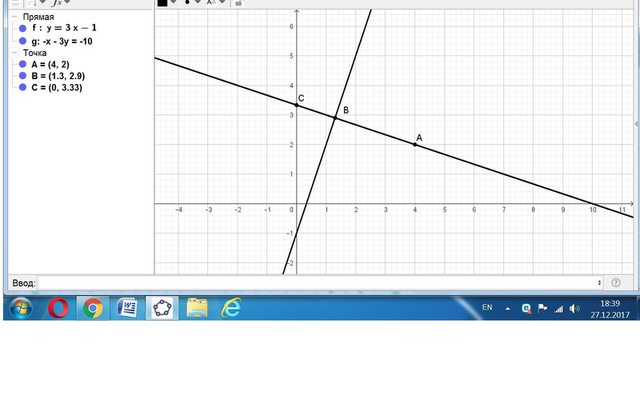
Будем считать, что уравнения прямых имеют вид:
- первое у = -2х + в,
- второе у = 3х - 1.
Но эти прямые не перпендикулярны, так как условие перпендикулярности:
к₂ = -1/к₁.
Перпендикулярность прямых от параметра в не зависит.
Он влияет только на ординату пересечения прямой оси Оу.
Так как одна прямая имеет точное определение уравнения у = 3х - 1 , то уравнение второй прямой представим в виде у = (-1/3)х + в.
Если бы были известны координаты любой точки на второй прямой, то, подставив их во второе уравнение, мы бы смогли определить значение параметра в. Тогда бы были получены точные уравнения двух перпендикулярных прямых.
Примем координаты точки А(4; 2), через которую проходит вторая прямая.
Подставим 2 = (-1/3)*4 + в.
Получаем в = 2 + (4/3) = 10/3.
Уравнение второй прямой: у = (-1/3)х + (10/3).
Этот пример приведен в приложении.