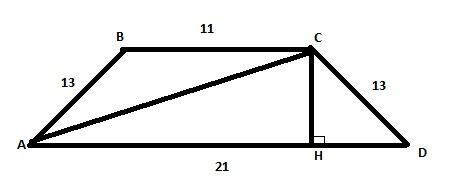
Пусть трапеция ABCD. AC-диагональ.
Нужно найти AC. BC=11, AD=21, AB=CD=13 см.
Используя формулу d1 = √h2 + m2
Где h-высота, m-сер.линия
Проведем высоту CH к основе AD.
Используя свойство равноб.трапеции узнаем, что отрезок HD-21-11/2=10/2=5см.
Отсюда из треуг.CHD(∠CHD=90°)
CH²=169-25=144, √144=12см.
Сер.линия=21+11/2=16см.
Подставляем:
d1 = √h2 + m2=√144+256=√400=20см
Ответ:20см.
// 2 Способ
Используя формулу
d1 = √с2 + ab=√169+21*11=√169+231=√400=20
P,S a и b - основания, с-сторона