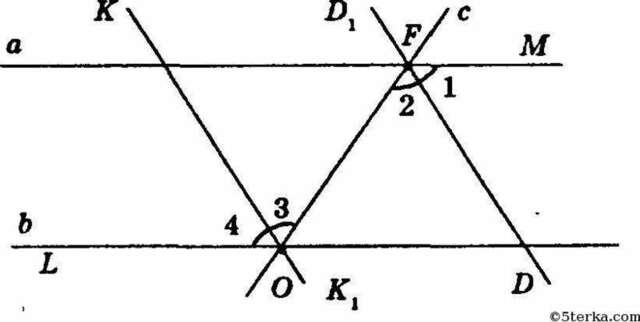
∠MFO = ∠FOL как внутренние накрест лежащие углы.
∠MFO = ∠1 + ∠2, ∠1 = ∠2, потому что FD — биссектриса.
∠FOL = ∠3 + ∠4, ∠3 = ∠4, потому что OK — биссектриса.
Таким образом, ∠1 = ∠2 = ∠3 = ∠4. Но ∠3 и ∠2 являются внутренними накрест лежащими при прямых DD1 и KK1 и секущей FO. Т.к .∠3 = ∠2, то прямые, содержащие биссектрисы, параллельны.