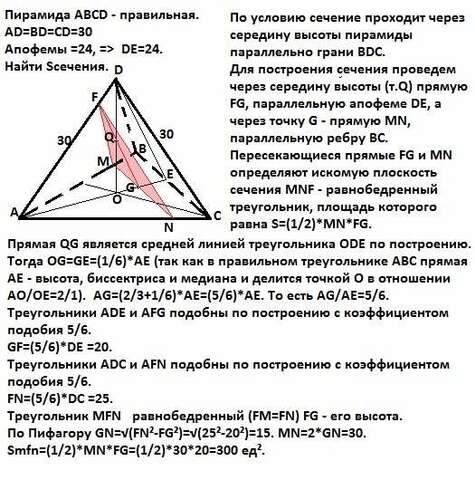
По условию сечение проходит через середину высоты пирамиды параллельно грани BDC.Для построения сечения проведем через середину высоты (т.Q) прямую FG, параллельную апофеме DE, а через точку G - прямую MN, параллельную ребру ВС. Пересекающиеся прямые FG и MN определяют искомую плоскость сечения MNF - равнобедренный треугольник (FM=FN), площадь которого равна S=(1/2)*MN*FG.
Прямая QG является средней линией треугольника ODE по построению. Тогда OG=GE=(1/6)*AE (так как в правильном треугольнике АВС прямая АЕ - высота, биссектриса и медиана и делится точкой О в отношении АО/ОЕ=2/1, считая от вершины и ОЕ=АЕ/3).
АG=(2/3+1/6)*АЕ=(5/6)*АЕ. То есть AG/AE=5/6.Треугольники ADE и AFG подобны по построению с коэффициентом подобия 5/6.
GF=(5/6)*DE =20.
Треугольники ADC и AFN подобны по построению с коэффициентом
подобия 5/6.
FN=(5/6)*DC =25.
Треугольник MFN равнобедренный (FM=FN) FG - его высота.По Пифагору GN=√(FN²-FG²)=√(25²-20²)=15. MN=2*GN=30.
Smfn=(1/2)*MN*FG=(1/2)*30*20=300 ед².
Или так:
В прямоугольном треугольнике DEC по Пифагору
СЕ=√(DC²-DE²)=√(600-576)=18. BC=36.
MN=(5/6)*BC=30 (из подобия треугольников АВС и АМN).
Smfn=(1/2)*MN*FG=(1/2)*30*20=300 ед².