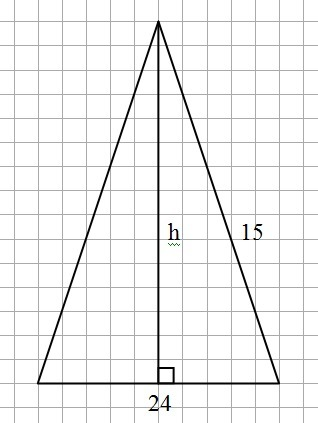
Равнобедренный треугольник высотой, проведенной к основанию, делится на два равных прямоугольных треугольника.
Прямоугольный треугольник, образованный высотой к основанию h, боковой стороной 15 и половиной основания 12:
1. Находим высоту, проведенную к основанию:
h = √(15²-12²) = √(225-144) = √81 = 9 (ед.)
2. Площадь исходного равнобедренного треугольника равна половине произведения основания на высоту, проведенную к основанию:
S = ah/2 = 24*9:2 = 108 (ед.²)
Ответ: 108 ед.²