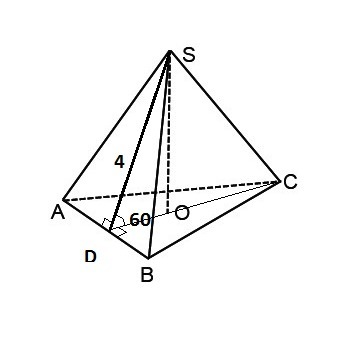
1, ΔDOS-прямоугольный; SO-высота пирамиды
SO=DS*sin SDC=4*sin60=4*√3/2=2√3
2.Если пирамида правильная, то основание АВС-равносторонний треугольник, О-центр вписанной и описанной окружности этого Δ, при этом DO-радиус вписанной окружности,а ОС-описанной.
О делит высоту основания в отношении ОС/OD=2:1
Из того же ,ΔDOS я найду OD=DS*cos60=4*0.5=2-это радиус вписанной окружности, тогда радиус описанной ОС=2OD=2*2=4
3. Сторона основания-это сторона равностороннего треугольника может быть найдена через радиус вписанной окружности
a=r*2√3=2*2√3=4√3
4. S(ABC)=a^2*sin60/2=(4√3)^2*√3/2*0.5=48*√3/4=12√3
5. боковыми гранями являются 2 равнобедренных треугольника с высотой 4 и основанием 4√3, площадь одного из них
S=ah/2=4√3*4/2=8√3
S(бок)=3*8√3=24√3
S(пол)=S(осн)+S(бок)-надеюсь ты разберешься и посчитаешь его сама...