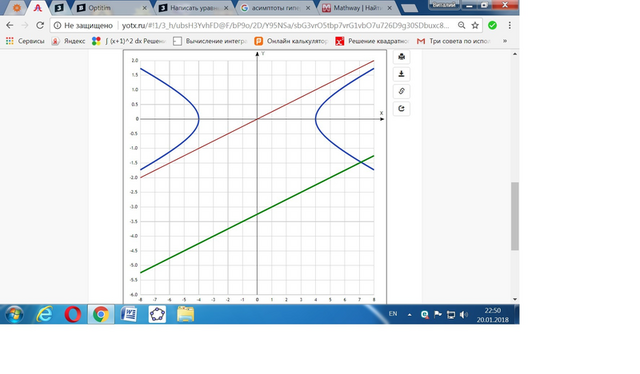
1) Дана точка А(5; -2) и гипербола x^2-16y^2=16.
Уравнение гиперболы выразим в каноническом виде.
(х²/4²) - (у²/1²) = 1.
Имеем a = 4 и b = 1.
Уравнение асимптоты гиперболы x^2-16y^2=16 с положительным угловым коэффициентом: у = (1/4)х.
Для параллельной прямой угловой коэффициент сохраняется.
у = (1/4)х + в.
Для определения параметра в подставим координаты точки А:
-2 = (1/4)*5 + в.
Отсюда в = -2 - (5/4) = -13/4.
Получаем уравнение прямой у = (1/4)х - (13/4).
График дан в приложении.
2) Так как одна сторона угла параллельна оси Ох, то угловой коэффициент его биссектрисы в уравнении прямой равен тангенсу угла наклона.
Выразим уравнение биссектрисы относительно у:
х - 2у + 6 = 0,
у = (1/2)х + 3. tg(α) = 1/2.
Вторая сторона угла имеет двойной угол наклона к оси Ох.
tg(2α) = 2tg(α)/(1 - tg²(α)) = 2*(1/2)/(1-(1/4)) = 1/(3/4) = 4/3.
Значит, к2 = 4/3.
Уравнение второй стороны угла у = (4/3)х + в.
Найдём вершину угла как точку пересечения у = 2 и х - 2у + 6 = 0.
Для этого подставим во второе уравнение у = 2:
х - 2*2 + 6 = 0,
х = -2, а у = 2 (точка пересечения лежит на прямой у = 2).
Для определения параметра в подставим эти координаты:
2 = (4/3)*(-2) + в,
в = 2 + (8/3) = 14/3.
Имеем уравнение второй стороны угла:
у = (4/3)х + (14/3).