2) Пожалуй, информация о том, что центром окружности, описанной около равностороннего треугольника является точка пересечения медиан, является лишней.
Центром окружности, описанной около треугольника, является точка пересечения его срединных перпендикуляров.
Срединными перпендикулярами любого равностороннего треугольника являются его высоты, они же медианы и биссектрисы.
Поэтому радиус R описанной около правильного треугольника окружности равен 2/3 его высоты h
h=a•sin 60°, где а - сторона треугольника, а углы равностороннего треугольника раны 60°.
h=6•√3/2=3√3
R=(3√3)•2/3=2√3 см
———————
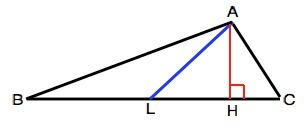
3) Медиана делит исходный треугольник на два, у которых основания равны, а высота, проведенная из общей вершины, является для них также общей. (см. рисунок)
S(ABL)=AH•DL/2
S(ACL)=AH•CL/2
Так как BL=CL, то площади этих треугольников равны, а площадь каждого равна половине площади ∆ АВС, т.е.18:2=9 см².
---------
Мы получили свойство медианы треугольника, которое полезно запомнить:
Медиана треугольника делит его на два равновеликих, т.е. на треугольники с равной площадью.