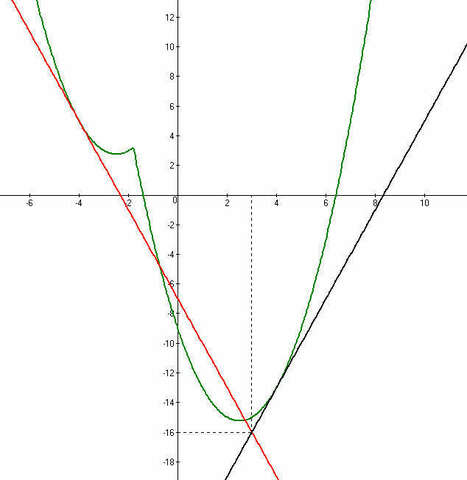
Найдите точку, пересечения касательных, поведенных к графику функций
f(x) = x² - |5x+9|
в точках х₁ = -4 и х₂ = 4.
Решение
Уравнение касательной к графику функции y = f(x) и проходящее через точку х₀ и у₀ определяется уравнением
у = f'(x₀)·(x - x₀) + y₀
где f'(x₀) - производная функции f(x) в точке х₀
Найдем производную в точке х₁=-4
В точке х₁ =-4 значение в модуле 5х+9 = 5(-4) + 9 = -20 + 9 < 0
следовательно модуль раскрываем поменяв знаки
|5x + 9| = -5x - 9
Запишем функцию при х₁ = -4
f(x) = x² + 5x + 9
Найдем производную
f'(x) = 2x + 5
Значение производной в точке х₁ = -4
f'(-4) = 2·(-4) + 5 = -8 + 5 = -3
Значение функции в точке касания
f(4) = 4² + 5·(-4) + 9 =16 - 20 + 9 = 5
Запишем уравнение касательной проходящей через точку х₁=-4;y(-4) = 5
y = -3(x + 4) + 5
y = -3x - 7
В точке х₂ = 4 значение в модуле 5х+9 = 5·4 + 9 = 20 + 9 > 0
следовательно модуль раскрываем не меняя знаки
|5x + 9| = 5x + 9
Запишем функцию при х₂ = 4
f(x) = x² - 5x - 9
Найдем производную
f'(x) = 2x - 5
Значение производной в точке х₂ = 4
f'(4) = 2·(4) - 5 = 8 - 5 = 3
Значение функции в точке касания
f(4) = 4² - 5·4 - 9 = 16 - 20 - 9 = -13
Запишем уравнение касательной проходящей через точку х₂= 4;y(4) =-13
y = 3(x - 4) - 13
y = 3x - 25
Найдем точку пересечения уравнений касательных решив систему уравний

Приравниваем правые части уравнений
-3х - 7 = 3х - 25
6х = 25 - 7
6х = 18
х = 3
y = 3x - 25 = 3·3 - 25 = 9 - 25 = -16
Следовательно точка пересечения касательных функции f(x) = x² - |5x+9|
в точках х₁ = -4 и х₂ = 4 находится в точке с координатами х=3; y=-16
Ответ: х=3; y=-16