Пожалуйста помогите! теорема 15.1 внизу написано дакозательство . и идёт описание оно...

Question

Пожалуйста помогите! теорема 15.1 внизу написано дакозательство . и идёт описание оно продолжается до следующего теоремы, мне очень нужно превратить в задачу , типо того решение и.т.д надеюсь понияли . Даю 20 баллов. Всем спасибо заранее, геометрия

---

Answer 1

Ох, просто начерти параллельные прямые и секущую, один угол равен столько, найти чему равен другой, делов то

Answer 2

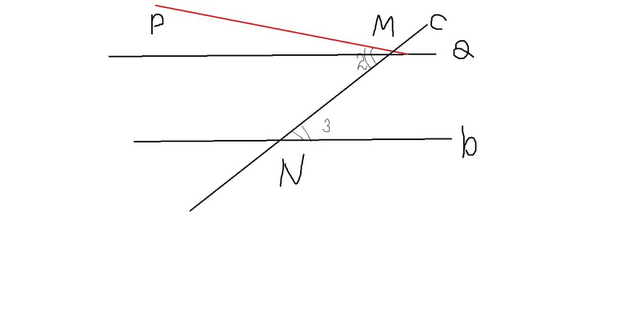
Если две параллельные прямые пересечены секущей,то накрест лежащие углы равны.

Дано:аIIb,MN-секущая.
Д-ть:у.1=у.2(НЛУ)
Д-во:способ от противного
Допустим,что у.1=у.2
Отложим от луча MN угол NMP,равный углу 2.По построению накрест лежащие углы NMP=углу 2-следовательно PM II b.
Получим,что через точку М проходят приямые (а и МР) параллельной прямой b!!! Это протеворечит аксиоме параллельных прямых.Значит наше допущение неверно!!!
у.1=у.2
Теорема доказана.


ой блин,я не прочитала внимательно,но мб тут что нб есть!!
удачи в геометрии,хотя в ней сама не шарю,хых

---