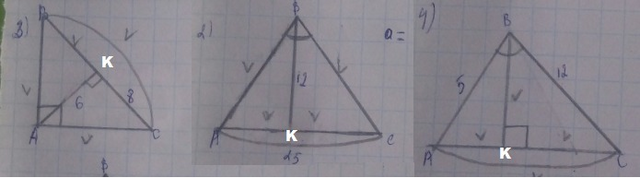
3) BK*KC = AK² ⇒ BK*8 = 36 ⇒ BK = 36/8 = 4,5
ΔABK - прямоугольный, ∠AKB = 90°. Теорема Пифагора
AB² = AK² + BK² = 6² + 4,5² = 36 + 20,25 = 56,25
AB = √56,25 = 7,5
ΔAKC - прямоугольный, ∠AKC = 90°/ Теорема Пифагора
AC² = AK² + KC² = 6² + 8² = 100
AC = √100 = 10
BC = BK + KC = 4,5 + 8 = 12,5
Ответ: BK = 4,5; AB = 7,5; AC = 10; BC = 12,5
2) Задача имеет смысл при условии, что
ΔABC - прямоугольный, ∠ABC = 90°, BK - высота
KC = AC - AK = 25 - AK
BK² = AK*KC ⇒ 12² = AK*(25 - AK) ⇒
144 = 25AK - AK²
AK² - 25AK + 144 = 0 - квадратное уравнение с неизвестной AK
D = 25² - 4*144 = 625 - 576 = 49 = 7²
AK = (25-7)/2 = 9 или AK = (25+7)/2 = 16
Так как 9+16 = 25 и AK ΔABK - прямоугольный, ∠AKB = 90°. Теорема Пифагора
AB² = AK² + KB² = 9² + 12² = 225
AB = √225 = 15
ΔCBK - прямоугольный, ∠CKB = 90°. Теорема Пифагора
CB² = CK² + KB² = 16² + 12² = 400
CB = √400 = 20
Ответ: AK = 9; KC = 16; AB = 15; CB = 20
4) Задача имеет смысл при условии, что
ΔABC - прямоугольный, ∠ABC = 90°. Теорема Пифагора
AC² = AB² + BC² = 5² + 12² = 169
AC = √169 = 13
BK = AB*BC / AC = 5 * 12 / 13 = 60/13 = 
ΔABK - прямоугольный, ∠AKB = 90°. Теорема Пифагора


Ответ: AC = 13;