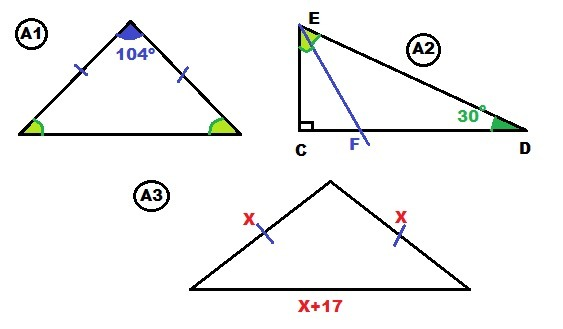
A1. 104° > 90° - тупой угол
Так как в равнобедренном треугольнике может быть только один тупой угол, значит, нужно найти углы при основании
(180° - 104°) : 2 = 76° : 2 = 38°
Два угла при основании равны по 38°
A2.
a) ∠С = 90°; ∠D = 30°
∠E = 90° - ∠D = 90° - 30° = 60°
EF - биссектриса ⇒ ∠DEF = 1/2 ∠E = 1/2 * 60° = 30°
ΔDEF : ∠DEF = ∠D = 30° ⇒ ΔDEF - равнобедренный
б) Биссектриса угла треугольника делит противолежащую сторону пропорционально прилежащим сторонам.
Так как катет CE меньше гипотенузы DE, значит, CF меньше DF:
CF < DF
A3. P = 77 см. Так как треугольник тупоугольный равнобедренный, то самая длинная сторона - основание ⇒
Пусть боковая сторона равна X см,
тогда основание равно Х + 17 см
Р = Х + Х + Х + 17 = 77
3X + 17 = 77
3X = 60
X = 20 см
X + 17 = 37 см
Стороны треугольника 20 см, 20 см, 37 см