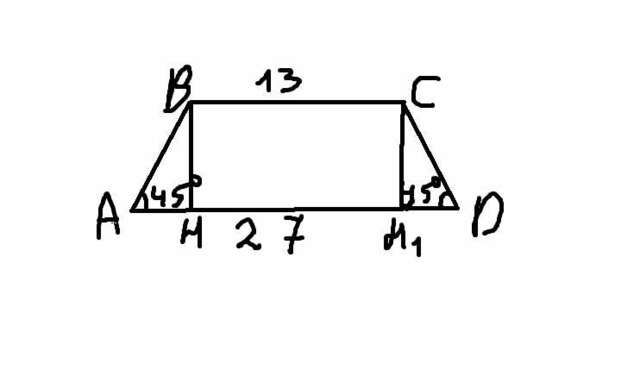
Площадь трапеции равна половине произведения ее оснований на высоту.
Проведем высоты BH и СН1, HBCH1 - прямоугольник ⇒ HH1=BC = 13 см
Δ ABH = ΔDCH1 по стороне и двум прилежащим к ней углам (AB=CD как боковые стороны равнобедренной трапеции, ∠A =∠D по условию, ∠H1CD= ∠HBA по сумме углов треугольника) ⇒
AH=H1D = (27-13)/2=7 см
в прямоугольном Δ ABH ∠ ABH = 90°-45° =45° (так как сумма острых углов прямоугольного треугольника 90°) ⇒ Δ ABH - равнобедренный ⇒
BH=AH=7 см
S (ABCD)=  *(27+13) *7=20*7=140 см²
*(27+13) *7=20*7=140 см²
Ответ: 140 см²