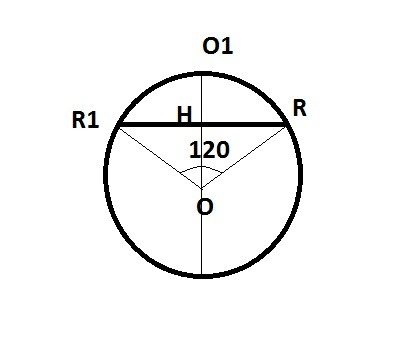
S=2piRh-площадь шарового сегмента, нужно найти R-вернее связь его с h
Рассмотрим ΔORR1-равнобедренный
Углы при основании по 30,гипотенуза ОR в ΔOHR вдвое больше ОН
Значит ОН=R/2; OH1=R/2
Выходит высота сегмента-половина радиуса шара
S=2pi*2H*H=4piH^2
Для нахождения площади сечения надо определить его радиус, из того же ΔOHR: r=HR=√(2H)^2-H^2)=H√3
S1=pir:2=3pi*H^2-площадь сечения