Квадрат и прямоугольник, площади которых соответственно равны 36 см² и54 см², имеют общую...

Question

Квадрат и прямоугольник, площади которых соответственно равны 36 см² и

54 см², имеют общую сторону, а угол между их плоскостями равен 30 °. Найти расстояние между параллельными сторонами прямоугольника и квадрата.

Квадрат і прямокутник, площі яких відповідно дорівнюють 36 см2 і
54 см2, мають спільну сторону, а кут між їх площинами дорівнює 30°. Знайти відстань між паралельними сторонами прямокутника і квадрата

Answer 1

Ответ: 96сантиметров

Answer 2

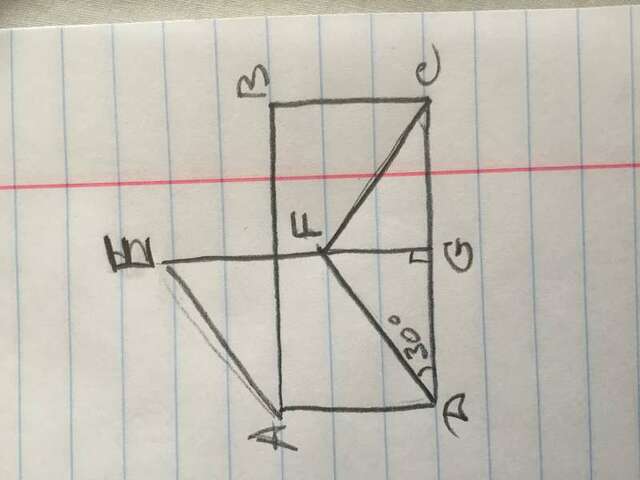
Пусть АEFD квадрат,
ABCD прямоугольник,
АD-общая сторона,
Найти: FC-?
Из точки F опустим перпендикуляр к DC и назовём эту точку G.
Тогда треугольники DFG и FCG - прямоугольные.
Сторона DF = 6 см ( квадратный корень из 36 см ). Так как Катет, противолежащий углу в 30˚, равен половине гипотенузы, то
FG= DF/2=6/2=3 см.
Из теоремы Пифагора:
c^2=a^2+b^2, где a,\;b – катеты, c – гипотенуза. Тогда
DG=корень из (DF^2 - FG^2)= корень из(36-9)=корень из 25 =5 см
DC= 54/6=9 cм (S прямоуг = а•b, площадь 54 из условия, а сторона АД= DF =6 см (строна квадрата, найденная выше). Тогда
CG=DC-DG= 9-5=4 см. Т. к. Треугольник FGC- прямоугольный (FG-перпендикуляр), то по теореме Пифагора
FC=корень из (FG^2+CG^2) = корень из (9+16)=корень из 25=5 см

---