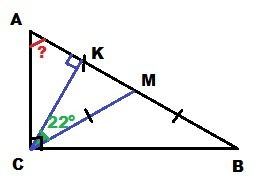
ΔABC : ∠ACB = 90°; AM = MB (CM - медиана); CK⊥AB
∠KCM = 22°
Медиана в прямоугольном треугольнике, проведённая из вершины прямого угла, равна половине гипотенузы ⇒
CM = 1/2 AB = AM = MB
ΔCKM : ∠CKM = 90° ⇒
∠KMC = 90°-∠KCM = 90°-22° = 68°
ΔAMC - равнобедренный (CM = AM) ⇒
∠A = ∠MAC = ∠ACM = (180° - ∠AMC)/2 = (180°- 68°)/2 = 56°
∠B = 90° - ∠A = 90° - 56° = 34°
∠A > ∠B
Ответ: больший острый угол равен 56°