Срочно!! Пожалуйста помогите!
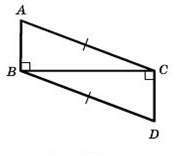
1) На рисунке АВ ⊥ ВС, CD ⊥ BC, AC = BD. Докажите, что АВ = CD.
2) Докажите равенство прямоугольных треугольников по катету и биссектрисе, проведенной из вершины прилежащего к этому катету острого угла.
3) Высоты АМ и СК треугольника АВС пересекаются в точке Н, НК = НМ. Докажите, то треугольник АВС равнобедренный.