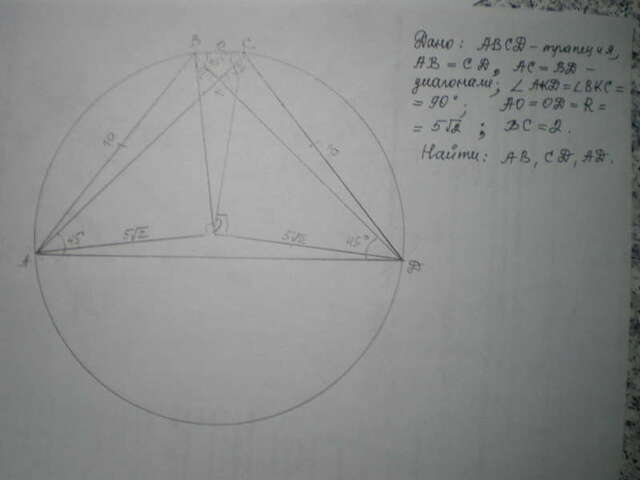
Решение:
Рассмотрим Δ ВСК - равнобедренный. ∠ВКС=90° (по условию)⇒∠ВСК=ВСК=45°.
ВК=КС=2sin45=√2
∠САД=∠ВСК=45° а ∠СДА=∠СВК=45° (как внутренние накрест лежащие при параллельных прямых ВС и АД)
Вписанный угол САД составляет половину центрального угла СОД, ⇒∠СОД=45*2=90°; ∠ВДА=1\2∠АОВ; ∠АОВ=90°.
Рассмотрим Δ АОВ и найдем АВ по теореме Пифагора:
АВ²=АО²+ОВ²=(5√2)²+(5√2)²=100; АВ=СД=√100=10.
Рассмотрим Δ ДКС - прямоугольный и найдем КД по теореме Пифагора:
КД²=СД²-КС²=100-2=98; КД=АК=√98.
Рассмотрим ΔАКД - прямоугольный и найдем АД по теореме Пифагора:
АД²=АК²+КД²=(√98)²+(√98)²=98+98=196; АД=√196=14.
Ответ: 10; 10; 14 ед.