ДАНО
F = x² - 4*x +3 - парабола
Y = k*x - 1 - прямая - одна точка касания
НАЙТИ
k = ? - коэффициент.
ДУМАЕМ
Это уже не просто прямая, а касательная к параболе.
Значение сдвига - b = - 1 - ДАНО !!!
РЕШЕНИЕ
Уравнение касательной по формуле
Y = F'(x)*(x- Xo) + F(Xo)
Xo = a
Преобразуем и получаем
Y = k*x + F(a) - F'(a)*a + F(a)
Отсюда находим выражение для сдвига - b.
b = F(a) - F'(a)*a = -1.
Находим производную функции
F'(a) = 2*a - 4
b = a² - 4*a + 3 - 2*a² + 4*a = -1
Упрощаем и получаем квадратное уравнение
a² = 4
Корни - а = +/- 2 - это координаты Х точки касания.
Находим значение производной в точке - а = х = - 2
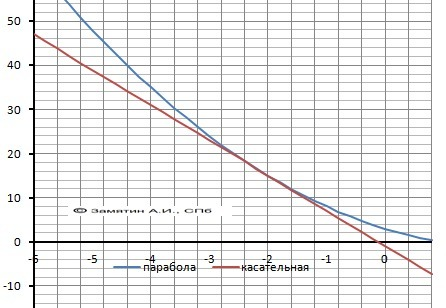
k = F'(-2) = -4 - 4 = - 8
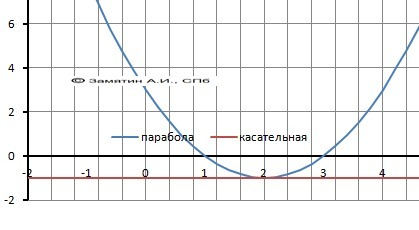
При Хо = 2 получаем k = 0
ОТВЕТ Одна точка касания при Х= -2 и Х = 2.
Графики на рисунках в приложении.