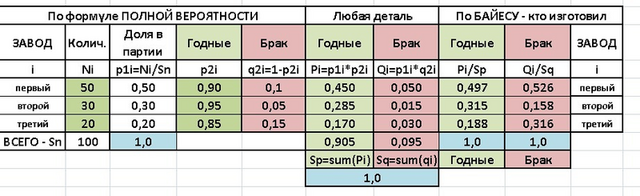
ТАБЛИЦА с расчетом в приложении - в ней всё, что надо для решения.
НАЙТИ - текст словами.
"И" выбрать случайную деталь "И" чтобы она оказалась годной, а не брак, при этом изготовлены они "ИЛИ" на 1-м "ИЛИ" на 2-м "ИЛИ" на 3-м заводе да ещё предположить где её изготовили.
РЕШЕНИЕ с комментариями.
1. Вероятности событий "И" - умножаются.
2. Вероятности событий "ИЛИ" - суммируются.
3. Наше событие состоит из двух - выбрать случайную и выбрать годную (она уже признана годной).
4. Применяем формулу ПОЛНОЙ ВЕРОЯТНОСТИ - сумма равна единице.
5. Вероятность выбрать годную - пропорциональна их количеству в партии - обозначаем p1i.
p11 = 50% = 0.5, р12 = 30%=0.3, p13 = 20% = 0.2 - даны.
Проверяем по формуле полной вероятности - сумма равна 100% = 1 - и это ПРАВИЛЬНО - других вариантов -нет.
6. Вероятность стандартной (годной) детали - р2i.
р21 = 0,9, р22 = 0,95, р23 = 0,85 - даны.
Вероятность БРАКА по формуле: q21 = 1 - p21 = 0.1, q22=0.05, q32 = 0.15.
7. Вероятность любой годной - по формуле - любая "И" годная - произведение:
Р1 = р11 * р21 = 0,5*0,9 = 0,45 - любая 1-го завода.
Не трудно вычислить вероятность любой бракованной.
Q1 = p11*q21 = 0.5*0.1 = 0.05. - это для 1-го завода.
8. Аналогично для 2-го и 3-го заводов.
P2 = 0.285, Q2 = 0.015 - для второго
P3 = 0.17, Q = 0.030 - для третьего.
9. По формуле "ИЛИ" находим вероятность годной в целом.
Sp = P1 + P2 + P3 = 0.905 = 90.5% - вероятность годной
Qp = 0.095 = 9.5% - вероятность брака.
Проверяем по формуле полной вероятности - сумма = 1 - правильно.
10. По формуле Байеса находим КТО изготовил.
Здесь используется формула
B1 = P1/Sp = 0.45 / 0.905 = 0.497 = 49,7% - на первом заводе
B2 = P2/Sp = 0.285/0.905 = 0.315 = 31.5% - на втором заводе - ОТВЕТ
B3 = P3/Sp = 0.17/0.905 = 0.188 = 18,8% - на третьем
Проверяем по формуле полной вероятности - 100%
ОТВЕТ: Эта годная деталь с вероятностью 31,5% изготовлена на втором заводе.
ДОПОЛНИТЕЛЬНО.
Из таблицы видно, что и первый и третий заводы выпускают больше брака, чем годных, а вот второй - меньше всего брака.