Решите пж (решить надо всё) за это задание вы получите 50 балов!

1). Соотношения между элементами прямоугольного треугольника:

$\displaystyle a^{2}+b^{2}=c^{2} \\ \\ h= \sqrt{b_{c}*a_{c}} \\ \\ b= \sqrt{b_{c}*c} \\ \\ a= \sqrt{a_{c}*c} \\ \\ c=a_{c}+b_{c}$

Тогда: h = BD = √(AD*DC) = √(12*16) = √192 = 8√3 (см)
                 BC = √(DC*AC) = √(16*28) = √448 = 8√7 (см)
                 AB = √(AD*AC) = √(12*28) = √336 = 4√21 (см)

2). Для построения отрезка произвольной длины с соотношением 2:7 , необходимо построить прямоугольный треугольник с гипотенузой, равной данному отрезку.
Зная, что a(c) = 2 и b(c) = 7, получим: a = √(a(c)*c) = √(2*9) = √18 ≈ 4,2
    b = √(b(c)*c) = √(7*9) = √63 ≈ 7,9
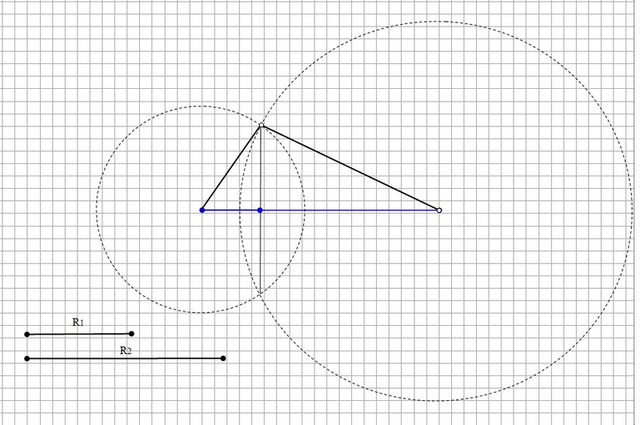
Строим две окружности с центрами в концах отрезка и радиусами,
кратными a и b. То есть R₁ = 4,2 см; 8,4 см; 12,6 см и т.д.
                                      и R₂ = 7,9 см; 15,8 см; 23,7 см и т.д.
Кратность подбирается такая, чтобы получить точку пересечения этих окружностей. Из этой точки опускаем перпендикуляр на отрезок. Полученная точка разделит отрезок в соотношении 2:7 (рис.2)