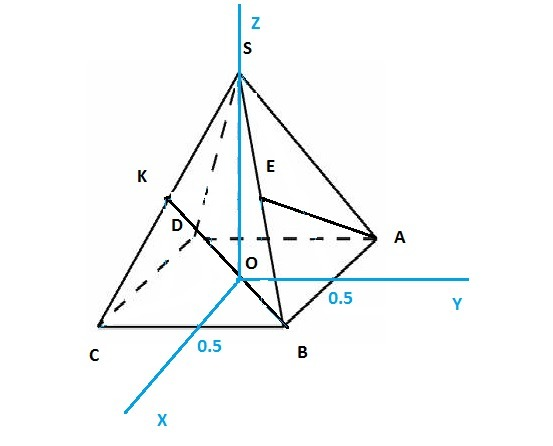
Если я найду координаты всех точек-задача будет легко решена через скалярное произведение векторов
Поэтому в введенной системе координат с центром в точке О(пересечение диагоналей квадрата со стороной 1)
вершины пирамиды имеют координаты
A(-1/2;1/2;0)
B(1/2;1/2;0)
C(1/2;-1/2;0)
D(-1/2;-1/2;0)
Для нахождения координат S рассмотрю прямоугольный ΔOBS
BS=1; OB=√2/2; OS^2=BS^2-OB^2=1^2-(√2/2)^2=1-0.5=0.5
Значит координаты S(0;0;1/2)
Осталось найти координаты К и Е. Это середины сторон SC и SB.
Е(1/4;1/4;1/4); K(1/4;-1/4;1/4)
|EA|^2=(1/4+1/2)^2+(1/4-1/2)^2+(0-1/4)^2=9/16+1/16+1/16=11/16
|EA|=√11/4
|EA|=|BK|- т.к. все ребра одинаковые
Найду координаты векторов ЕА и ВК
ЕА=(-1/2-1/4;1/2-1/4;0-1/4)=(-3/4;1/4;-1/4)
KB=(1/2-1/4;1/2+1/4;0-1/4)=(1/4;3/4;-1/4)
запишу скалярное произведение их
-3/4*(1/4)+1/4*(3/4)+(-1/4)*(-1/4)=-3/16+3/16+1/16=1/16-это в координатах
|EA|*|KB|*cosx=11/16*cosx
приравнивая их получу
11/16*сosx=1/16
cosx=(1/16)/(11/16)=1/11≈0.09
arccos(0.09)≈≈85 градусов