Общая хорда двух пересекающихся окружностей является стороной правильного треугольника,...

Question

Общая хорда двух пересекающихся окружностей является стороной правильного треугольника, вписанного в одну окружность, и стороной правильного шестиугольника, вписанного в другую окружеость. Длина этой хорды равна а. Найдите расстояние между центрами окружностей если она лежит по одну сторону от хорды.
Расписать.

Comments

Центры окружностей лежат по одну сторону от хорды.

Answer 1

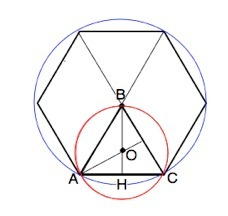
Правильный шестиугольник состоит из 6 правильных треугольников со сторонами, равными данной хорде. т.е. а. 
Если центры окружностей лежат по одну сторону от данной хорды, а хорда - общая сторона этих многоугольников, то вершина В треугольника АВС совпадает с центром шестиугольника, и расстояние между их центрами равно радиусу окружности, описанной около правильного треугольника ( см. рисунок вложения). 
ВО=r=а/√3

---