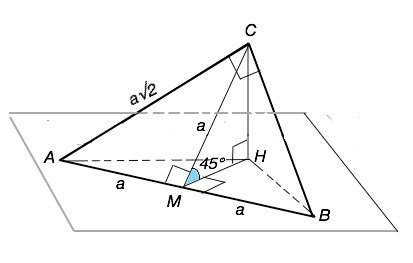
Пусть α – плоскость, проведенная через гипотенузу ∆ АВС под углом 45°.
Угол между плоскостью треугольника и плоскостью, проведенной через гипотенузу –двугранный и равен линейному углу между лучами. проведенными в плоскостях двугранного угла перпендикулярно к одной точке на его ребре. т.е. на гипотенузе АВ.
Опустим СН перпендикулярно плоскости альфа.
Проведем СМ⊥АВ.
СМ- высота и медиана равнобедренного ∆ АВС.
МН - проекция СМ на плоскость α.
По ТТП отрезок МН⊥АВ. ⇒
Угол СМН - данный и равен 45°
Примем АВ=2а, тогда по свойству медианы прямоугольного треугольника СМ=АВ:2=а.
Острые углы равнобедренного прямоугольного треугольника равны 45°.
Катеты АС=ВC=АМ:sin45°=а√2
∆ СМН - прямоугольный, угол СМН=45° (дано).
СН=МН=СМ•sin45°=a•√2/2=а/√2
В равных ∆ АСН и ∆ ВСН катеты треугольника АВС –наклонные АС и ВС.
sin∠CAH=BH:AC= (a/√2):a√2=1/2– 'это синус 30°
∠СВН=∠САН=30°