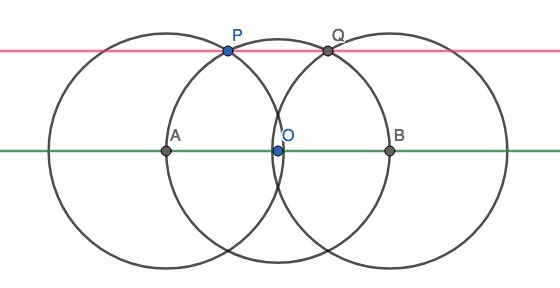
Построение: возьмем точку O на прямой, которая точно не лежит на перпендикуляре (это можно сделать на глаз без измерений), проведем окружность с центром в точке O и радиусом OP, где P – данная точка. Эта окружность пересекает прямую в двух точках A и B. Проведем окружности с центром с точке A и радиусом AP и с центром в точке B и радиусом AP. Последняя окружность пересекает первую в некоторой точке Q, прямая PQ – искомая.
Доказательство:
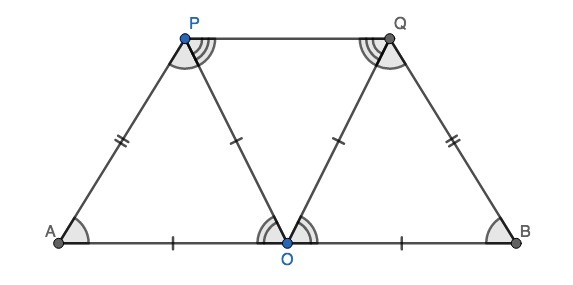
Равнобедренные треугольники APO и BQO равны по трём сторонам, тогда отмеченные на чертеже углы равны.
Пусть ∠A = α, тогда ∠AOP = ∠BOQ = 180° - 2α; ∠POQ = β = 180° - 2∠AOP = 4α - 180°. Отсюда ∠OPQ = (180° - β)/2 = 180° - 2α.
Углы ∠AOP и ∠OPQ оказались равны, а так как это накрест лежащие углы при прямых AB и PQ и секущей PO, то AB || PQ, что и требовалось доказать.