В треугольнике АВС биссектриса ВК является его высотой. Найдите периметр треугольника...

Question

В треугольнике АВС биссектриса ВК является его высотой. Найдите периметр треугольника АВС, если периметр треугольника АВК равен 16 см и ВК = 5 см.


25 см

20 см

21 см

22 см








В треугольнике DEF известно, что ∠EDF=68°, ∠DEF=44°. Биссектриса угла EDF пересекает сторону EF в точке K. Найдите угол DKF.


78°

102°

34°

68°








Серединный перпендикуляр стороны ВС треугольника АВС пересекает сторону АВ в точке D. Найдите отрезок AD, если CD = 4 см, АВ = 7 см.


7 см

3 см

5 см

4 см

Answer 1

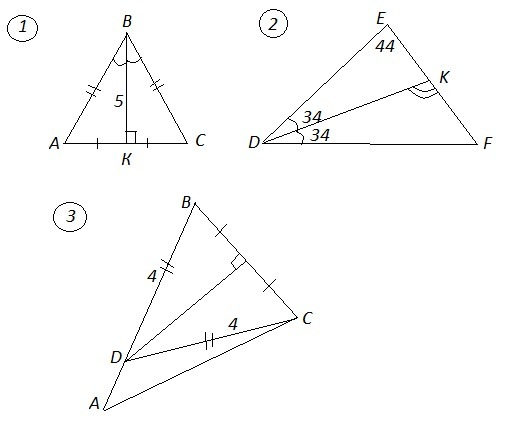
1)  Если в треугольнике биссектриса ВК является ещё и высотой, то этот треугольник равнобедренный и  АВ=ВС.
Р(АВК)=16  , Р(ВКС)= Р(АВК) , так как ΔАВК=ΔВКС по двум сторонам и углу между ними (АВ=ВС , ВК - общая , ∠АВК=∠СВК)
Р(АВС)=Р(АВК)+Р(ВСК)-2*ВК=2*Р(АВК)-2*5=2*16-10=22

2)  ΔDEF:  ДК - биссектриса  ⇒  ∠КDЕ=∠КDF=68°:2=34°
  ∠F=180°-(∠EDF+∠DEF)=180°-(68°+44°)=68°
ΔDKF:  ∠DKF=180°-(∠KDF+∠DFK)=180°-(34°+68°)=78°

3)  Точки, лежащие на серединном перпендикуляре к отрезку, равноудалены от концов этого отрезка  ⇒  DC=DB=4 см.
АВ=AD+DB=AD+4  ⇒  AD=AB-4=7-4=3 (см) .

---