Задание 1.
1. √37 Число двузначное и нужно приближенное значение, поэтому проще использовать способ древних вавилонян:
 ≈
≈ 
 ≈
≈  ≈ 6,08(3)
≈ 6,08(3)
С округлением √37≈ 6,08
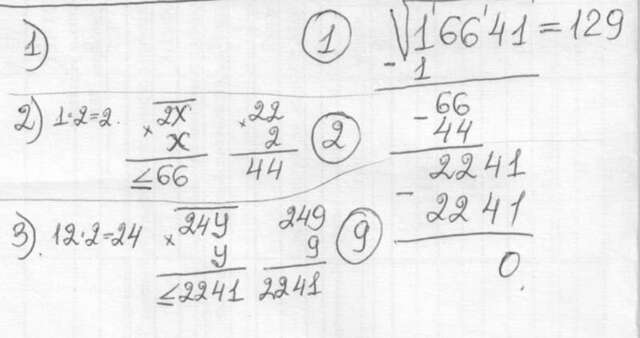
2. √16641 - искать ближайший в этому числу квадрат не имеет смысла(число само является квадратом). Так что приведу метод, который когда-то показывали в университете.
1) разбить число по парам цифр от младшего. Из старшей единицы извлечь максимальный корень - 1, вычесть, снести 66
2) умножить 1 на 2, к полученной двойке нужно справа дописать такую цифру, чтобы при умножении на эту цифру получилось число, не большее 66. Такой цифрой будет 2. Записать 2 в ответ, из 66 - 22*2 = 22. Снести оставшиеся 41
3) Число в ответе 12 умножить на 2 = 24. Справа нужно дописать такую цифру, чтобы при умножении на эту цифру получилось число, не большее 2241. Такая цифра 9. Записать в ответ.
Вычесть 2241 - 249*9 = 0.
√16641 = 129
Задание 2.
1. x² = -40 - для x∈R решений не имеет
2. x² = 361; x₁ = 19; x₂ = -19
3. (x² + 5)² = 144
1) x² + 5 = 12 или 2) x² + 5 = -12
x² = 7 x² = -17 - для x∈R решений не имеет
x₁ = √7; x₂ = -√7