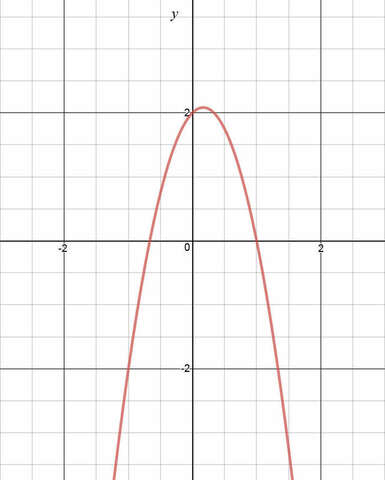
Найдите наибольшее значение функции:
y=|x-2|+2x-3x²
Решение
По определению модуля

Поэтому можно записать

Определим производный кусочно заданной функции
При х ≥ 2
y' = (3x - 2 - 3x²)' = 3 - 6x
При х ≥ 2 производная на интервале [2;+∞) будет отрицательной y'<0.<br>Следовательно функция
y=|x-2|+2x-3x²
на интервале [2;+∞) убывает.
Найдем производную на интервале (-∞;2)
y' = (2 + x - 3x²)' = 1 - 6x
Найдем критическую точку приравняв производную к нулю.
y' = 0 ⇔ 1 - 6x = 0
x =`1/6
На числовой прямой отобразим эту точку и определим знаки производной
+ 0 -
---------------------!----------------!
1/6 2
На интервале (-∞;1/6] производная больше нуля и функция возрастает.
На интервале [1/6;2] производная меньше нуля и функция убывает.
В точке х=1/6 функция имеет максимум.

Ответ: ymax = y(1/6) = 25/12