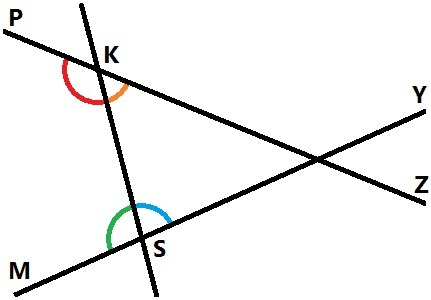
1) Внутренние углы лежат между прямыми PZ и MY. При пересечнии двух прямых секущей образуется четыре внутренних угла.
а) Накрест лежащие углы лежат по разные стороны от секущей.
∠PKS, ∠KSY
∠ZKS, ∠KSM
б) Односторонние углы лежат по одну сторону от секущей.
∠PKS, ∠KSM
∠ZKS, ∠KSY
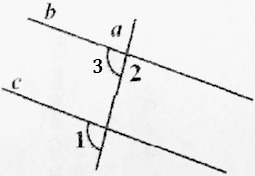
2) ∠3=∠1 =93° (соответственные углы при параллельных равны)
∠2=180°-∠3 =180°-93° =87° (смежные углы составляют развёрнутый угол, 180°)
3) Внутренний угол a, смежный с ним внешний угол 14a. Смежные углы составляют развёрнутый угол, 180°.
a +14a =180° <=> 15a=180° <=> a=180°/15 =12°
Углы при основании равнобедренного треугольника равны. Сумма углов треугольника 180°. Если углы при основании равны 12°, то угол противолежащий основанию равен 180°-2*12° =156°
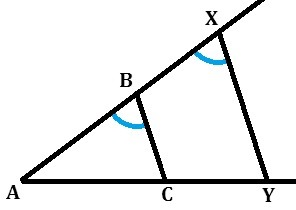
4) Треугольники ABC, AXY - равнобедренные, углы при основаниях равны.
∠ABC=(180°-∠A)/2, ∠AXY=(180°-∠A)/2 => ∠ABC=∠AXY
При пересечении прямых BC и XY секущей AX соответственные углы равны, следовательно прямые параллельны.
ИЛИ
Обратная теорема Фалеса: если прямые отсекают на сторонах угла пропорциональные отрезки, начиная от вершины, то прямые параллельны.
Длины BX и CY равны, так как получены вычитанием равного из равного: BX=AX-AB, CY=AY-AC => BX=CY.
AB/AC=BX/CY =1
Прямые BC и XY отсекают на сторонах угла пропорциональные отрезки, следовательно параллельны.