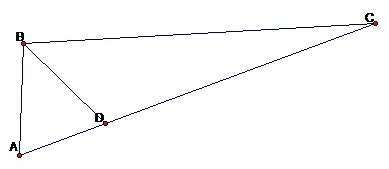
На рисунке обозначения другие.
Несколько способов существует. Докажем через отношение площадей.
Треугольники имеют общую вершину, их площади относятся как их основания: S(ABD) : S(DBC) = AD : DC.
У этих треугольников равные углы, поэтому отношение площадей равно отношению произведений сторон, образующих эти равные углы.
S(ABD) : S(DBC) = (AB*BD) :( BD*BC) = AB : BC.
И получаем AD: DC = AB:BC).