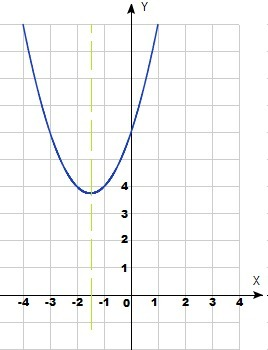
1 способ : графический
f(x) = x²
+ 3x + 6 - квадратичная парабола, ветви направлены вверх. Левая половинка до вершины параболы будет убывать, правая половинка параболы будет возрастать. Функция непрерывна на всей области определения.
Координата вершины параболы
x₆ = -b/(2a) = -3/2 = -1,5
Промежуток убывания функции x∈(-∞; -1,5]
Промежуток возрастания функции x∈[-1,5; +∞)
2 способ : вычисление первой производной
f'(x) = (x² + 3x + 6)' = 2x + 3 = 0
x = -1,5 - точка экстремума функции
x ∈ (-∞; -1,5] f'(x) < 0 ⇒ функция убывает
x ∈ [-1,5; +∞) f'(x) > 0 ⇒ Функция возрастает