Дано угол ACB=90градусов:CD|AB:BD=16см:CD=4 см Найти AD,AC,BC.

Question

Дано угол ACB=90градусов:CD|AB:BD=16см:CD=4 см Найти AD,AC,BC.

Comments

AB:BD это значит, что одно число разделили на другое?

Answer 1

 По теореме Пифaгора CB=4^2+16^2=4 корня из 17 (^2-возвести в квадрат. ) Рассмотрим треугольники ABC и CBD, они подобны. CB(изABC)/DB(изCDB)=AC(изABC)/CD(изCDB) неизвестная АС.

 АС=(CB*CD)/DB. Подставим АС=(4корня7*4)/16=корень из 17. так же AB(изABC)/CB(изCDB)=CB(изABC)/DB(изCDB) AB=(CB*CB)/DB=(4 корня из 17*4 корня из 17)/16=17. AB=AD-DB=17-16=1

Comments

в конце ошибка. ищем AD, а у вас АВ

Answer 2

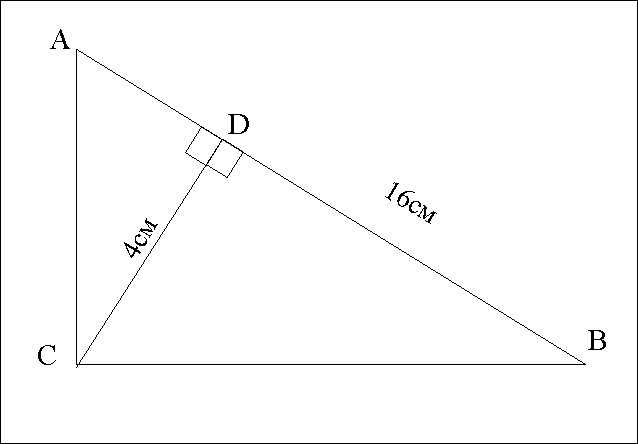
Дано:
ΔАВС
∠С  = 90°
CD⊥AB;
BD=16см;
CD=4 см.
Найти AD; AC; BC. 
Решение.
1) CD⊥AB, значит, ΔACD и ΔBCD  - прямоугольные.

2) Применим теорему Пифагора для ΔВСD.
СD² + ВD² = ВС²
4² + 16² = ВС²
ВС² = 16 + 256 = 272
ВС = √272
ВС = 4√17 см

3) Высота в прямоугольном треугольнике, проведенная из вершины прямого угла, разбивает прямоугольный треугольник на два подобных треугольника.
ΔBCD подобен ΔACD.
Значит, соответствующие стороны пропорциональны:
BD : CD = BC : AC
16 : 4 = 4√17 : AC
АС = 4·4√√17: 16
АС = √17 см

4) Применим теорему Пифагора для ΔАСD.
СD² + АD² = АС²
AD² = AC² - CD²
AD² = √17² -  4² = 17 - 16 =1
AD ² = 1
AD = √1 = 1
AD = 1 cм 

Ответ: AD = 1см;   AC = √17см;  BC=4√17 см. 

---