1) Касательная KL перпендикулярна радиусу OK. OKL - прямоугольный треугольник. Катет против угла 60° равен другому катету, умноженному на √3.
KL=OK√3 =6√3
2) Касательная NM перпендикулярна радиусу ON. ONM - прямоугольный треугольник. Катет против угла 30° равен половине гипотенузы. ON=OM/2 => ∠NMO=30°. Касательные из одной точки составляют равные углы с прямой, проходящей через эту точку и центр окружности.
∠NMK=2∠NMO =30°*2 =60°
3) Треугольник OAB - равносторонний (OA=OB - радиусы), ∠OAB=60°. Касательная AC перпендикулярна радиусу OA, ∠OAС=90°.
∠BAC=∠OAC-∠OAB =90°-60° =30°
4) ∠BAM найден в задаче (3) =30°. Отрезки касательных из одной точки равны, AM=BM, △AMB - равнобедренный, ∠BAM=∠ABM.
∠AMB=180°-2∠BAM =180°-30°*2 =120°
5) Касательная MN перпендикулярна радиусу OM. OMN - египетский треугольник (3:4:5) cо множителем 3 (OM=4*3; ON=5*3). MN=3*3=9
6) Отрезки касательных из одной точки равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. △MKO=△NKO (по двум сторонам и углу между ними), ∠MOK=∠NOK= ∠MON/2 =60°.
Касательная MK перпендикулярна радиусу OM. OMK - треугольник с углами 30°, 60°, 90°: стороны равны с/2, с√3/2, с (гипотенуза). Катет против угла 60° равен с√3/2.
MK=NK= OK√3/2 =3√3
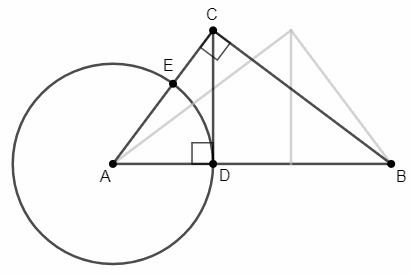
7) Касательная CD перпендикулярна радиусу AD, ∠ADC=90°.
По теореме о высоте из вершины прямого угла: AC^2=AB*AD
По теореме Пифагора: AC^2=AD^2 +CD^2
AD^2 +CD^2=AB*AD <=>
AD^2 -AB*AD +CD^2 =0 <=>
AD₁₂= 25±√[(25+24)(25-24)] /2 =[25±7]/2 <=>
AD₁=16; AD₂=9
AE=AD (радиусы), AE= {9; 16}
8) Касательная BM перпендикулярна радиусу OB. OBM - прямоугольный треугольник. Катет OB равен половине гипотенузы OM, следовательно лежит против угла 30°. ∠OMB=30°. Касательные из одной точки составляют равные углы с прямой, проходящей через эту точку и центр окружности. ∠AMB=2∠OMB =60°