Общая схема для построения
графиков функций.
1. Найти область
определения функции D(y).
Заданную функцию представим в виде:

Отсюда видим 2 точки разрыва функции: х = 1 и х = -1.
Тогда D(y) = R, x ≠ 1, x ≠ -1.
2. Найти точки пересечения
графика функций с осями координат.
Есть только одна точка пересечения графика с осями х и у - это точка х = 0, у = 0.
3. Исследовать функцию на
четность или нечетность.
f(x) ≠ f(-x), следовательно, f(x) является функцией общего вида.
4. Исследовать функцию на
периодичность - не периодична.
5. Найти промежутки
монотонности и точки экстремума функции.
Производная функции равна y' = (x² + 1)/((1-x²)²).
Переменная в квадрате - значит, производная только положительна, а функция возрастает на всей области определения.
Производная не может быть равна нулю - поэтому нет ни минимума, ни максимума функции.
6. Найти промежутки
выпуклости и точки перегиба функции.
Вторая производная равна:
 .
.
Отсюда видно, что ноль её равен при х = 0.
То есть, точка (0; 0) - это точка перегиба графика функции.
7. Найти асимптоты функции.
Асимптоты - линии разрыва х = 1 и х = -1 и ось Ох.
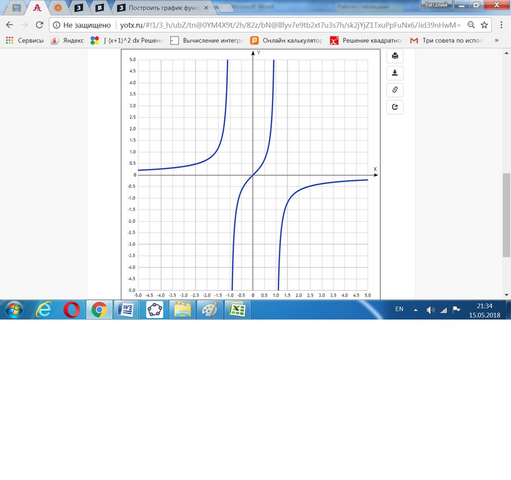
8. По результатам исследования построить график .
Таблица точек: f(x)=x/(1−x²)xy-5.0 0.21 -4.5 0.23 -4.0 0.27 -3.5 0.31 -3.0 0.38 -2.5 0.48 -2.0 0.67 -1.5 1.2 -1.0 - -0.5 -0.67 0 0 0.5 0.67 1.0 -1.5 -1.2 2.0 -0.67 2.5 -0.48 3.0 -0.37 3.5 -0.31 4.0 -0.27 4.5 -0.23 5.0 -0.21