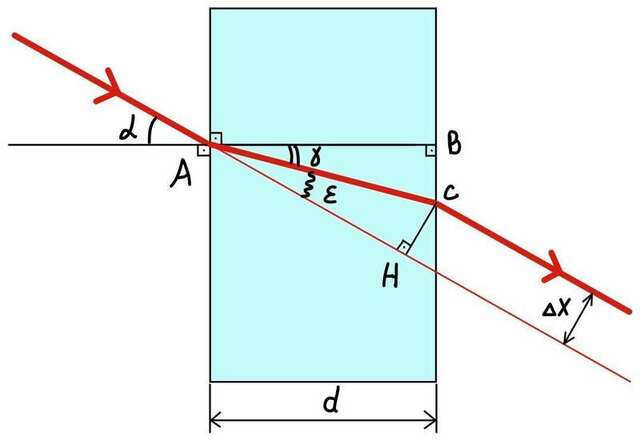
Я сделал пясняющий рисунок. Буду писать решение, опираясь на обозначения рисунка:
α = 30° – угол падения луча;
γ – угол преломления луча.
Из рисунка видно, что угол ε – это разность угла падения и угла преломления.
Отрезок CH равен данному смещению Δx = 2 мм.
Отрезок AB равен толщине пластинки d, поэтому его я и буду искать.
По закону преломления:
sinα / sinγ = n, отсюда
sinγ = sinα / n,
sinγ = sin30° / n,
sinγ = 0,5 / 1,73,
sinγ = 0,289,
γ ≈ 16,8° (рассчитано на калькуляторе путём взятия арксинуса от 0,289)
Угол ε = α - γ = 13,2°.
В прямоугольном треугольнике AHC:
sinε = CH / AC
AC = CH / sinε
В прямоугольном треугольнике ABC:
cosγ = AB / AC
AB = AC * cosγ
Тогда:
AB = (CH / sinε) * cosγ
То есть
d = (Δx / sinε) * cosγ
Подставлю Δx в миллиметрах, тогда и толщина пластинки d получится в миллиметрах.
d = (2 мм / sin(13,2°)) * cos(16,8°)
d ≈ (2 мм / 0,228) * 0,957
d ≈ 8,4 мм.
Ответ: d = 8,4 мм.