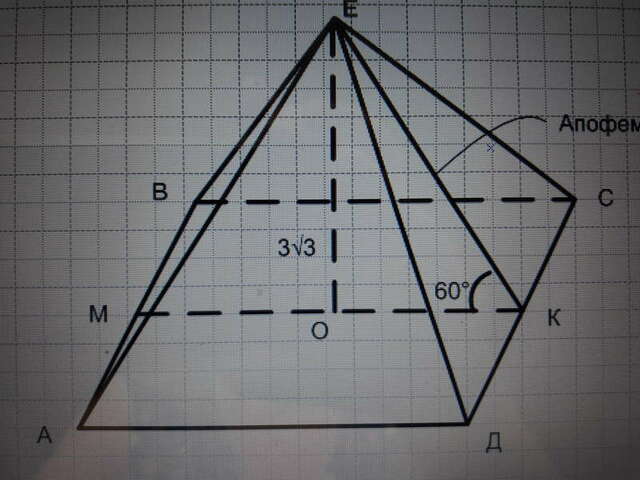
1) Смотрим на рисунок и находим длину апофемы ЕК из соотношения:
Sin 60°= OE/EK
EK = OE/Sin 60° = 3√3/(√3/2) = 6 см
2) Находим ОК из соотношения:
Cos 60°= OK/EK
OK = EK*Cos 60°= 6*0,5 = 3 см
3) Так как пирамида правильная, то основанием является квадрат, значит:
2*ОК = МК = ВС = АД = АВ = СД = 2*3 = 6 см
4) Находим площадь основания:
S(осн) = АВ*АД = 6*6 = 36 см²
5) Находим площадь боковой грани, которая представляет собой равнобедренный треугольник, высота которого равна длине апофемы ЕК (6 см), а основание равно СД (6 см)
S(гр) = (1/2)*СД*ЕК = (1/2)*6*6 = 18 см²
6) Так как граней 4, то общая площадь поверхности пирамиды равна:
S(пир) = S(осн) + 4*S(гр) = 36 + 4*18 = 108 см²