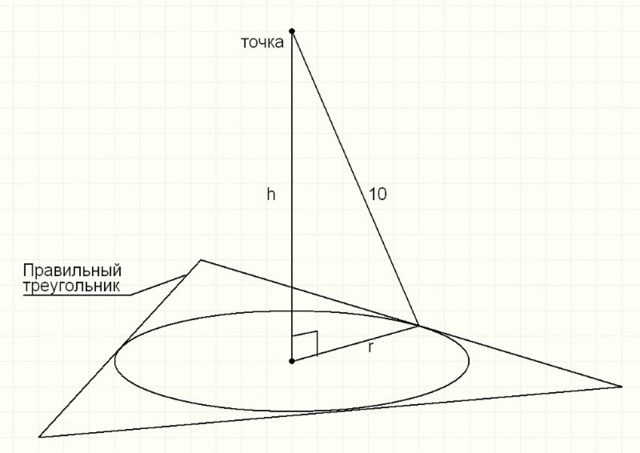
Периметр P правильного треугольника равен 36 см, а расстояние от некоторой точки до каждой из сторон треугольника 10см. Найдите расстояние от этой точки до плоскости треугольника.
Из заданной точки опускаем перпендикуляр h к плоскости треугольника. h - расстояние от этой точки до плоскости треугольника. Так как заданная точка равноудалена от каждой стороны треугольника, то и каждая точка перпендикуляра h тоже равноудалена от каждой стороны треугольника.
На плоскости треугольника точка, равноудаленная от каждой сторон - это центр вписанной окружности.
Радиус вписанной окружности r правильного треугольника
r = P / 6√3
h находим по теореме Пифагора
h = √( 10² - r² )
h = √( 10² - (P / 6√3)² )
h = √( 10² - (36 / 6√3)² ) = 2 √22 ( ≈ 9.38 ) см