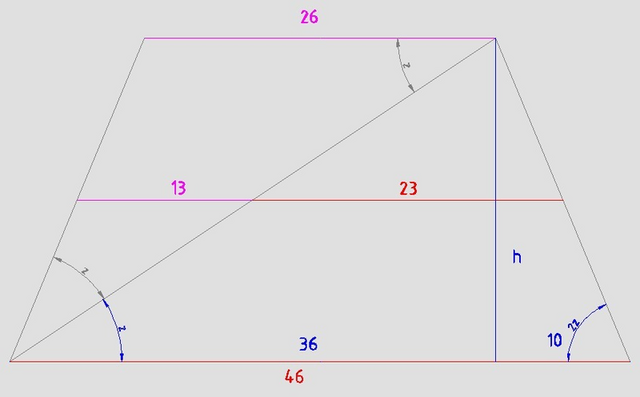
Отрезки, на который бьётся средняя линия в 2 раза меньше оснований
a = 23*2 = 46
b = 13*2 = 26
Угол между диагональю и основаниями - z
Угол между диагональю и боковой стороной - тоже z
Угол между нижним основанием и боковой стороной - 2z
Проекция боковой тсороны на основание (a-b)/2 = (46-26)/2 = 10 см
остаток нижнего основания 46-10 = 36 см
Для поиска высоты составим два уравнения
h/36 = tg(z)
h/10 = tg(2z)
----
18*tg(z) = 5*tg(2z)
18*tg(z) = 5*2tg(z)/(1-tg²z)
9(1-tg²z) = 5
9 - 9*tg²z = 5
4 - 9*tg²z = 0
(2 - 3*tg z)(2 + 3*tg z) = 0
tg z = 2/3
h/36 = tg(z)
h/36 = 2/3
h = 24
второй корень
tg z = -2/3
Приведёт к отрицательной высоте, нам такого не надо.
Итого, высота 24 см
Площадь
S = 1/2*(46 + 26)*24 = 864 см²