Вычислить площадь фигуры, ограниченной линиями

Question

Вычислить площадь фигуры, ограниченной линиями

---

Comments

ну хотя да, там просто определенным интегралом, это я напутал)

---

ну попробуй реши, мне то это не очень надо

---

а зачем вы тогда столько баллов даете если это вам не очень надо)

---

Вы это кому? Я ничего такого не писал

---

а, перепутал блин)

---

я не автор

---

вопрос , если я кину задание по дифференциальным уравнениям вы сможете решить?

---

нет уж, 10 минут прошли- я решаю

---

ну попробуйте киньте

---

больше я в ваши разборки ни ногой...

Answer 1

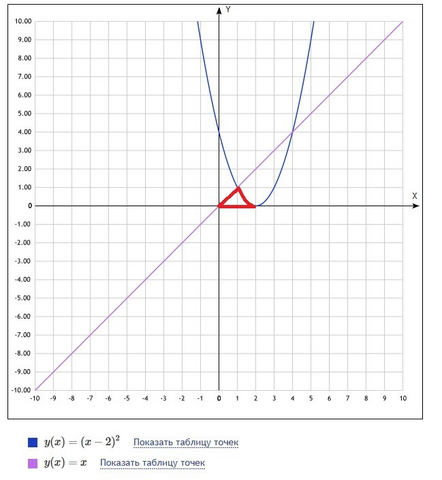
Полученную фигуру можно разделить на 2 части:прямоугольный треугольник с катетами 1 и 1, его S1=1/2 и криволинейный треугольник, его площадь вычислю через интеграл
S2=∫(x^2-4x+4)dx=x^3/3-4x^2/2+4x=x^3/3-2x^2+4x=
пределы интегрирования по х от 1 до 2
=8/3-8+8-(1/3-2+4)=8/3-2 1/3=1/3
S=S1+S2=1/2+1/3=5/6

---

Comments

еще вопросы есть?

---

если решения не будет минут 10-я распишу

---

ну дорешивайте тогда уже, в чем проблема)

---

у меня нет...

Answer 2

Надеюсь правильно решил)) 

---

Comments

Да блин, неправильно решил, там минус потерял, кароче сейчас тебе вон знаток решит))

---

Там кароче будет 8/3 - 1/3 -4 +2 - 8 -4 = 1/3 И в площадь будет 8/15