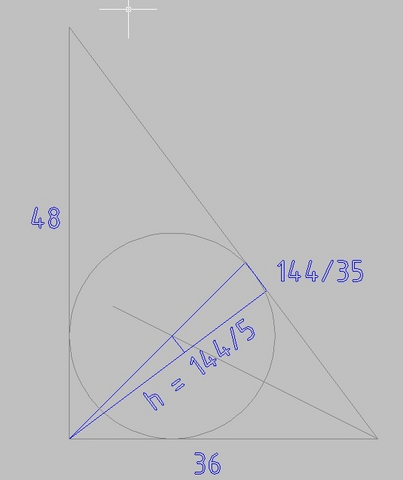
Гипотенуза (по теореме Пифагора)
с² = 48² + 36² =2304 + 1296 = 3600
с = 60
Площадь через катеты
S = 1/2*36*48 = 864
Полупериметр
p = 1/2(36 + 48 + 60) = 72
Площадь через полупериметр и вписанную окружность
S = rp
864 = r*72
r = 12
---
Площадь через гипотенузу и высоту
S = 1/2*h*60 = 864
h = 144/5
---
Короткий отрезок гипотенузы, отсекаемый высотой, найдём по т. Пифагора
x² + h² = 36²
x² + (144/5)² = 36²
x² + 20736/25 = 1296
x² = 11664/25
x = 108/5
---
Короткий отрезок гипотенузы y, отсекаемый биссектрисой прямого угла найдём из пропорциональности отрезков, на которые биссектриса делит противолежащую сторону прилежащим сторонам
y/36 = (60-y)/48
4y = 180 - 3y
7y = 180
y = 180/7
Расстояние между точками пересечения с гипотенузой высоты и биссектрисы
z₂ = y - x = 180/7 - 108/5 = (180*5 - 108*7)/35 = (900 - 756)/35 = 144/35
В больном синем треугольнике не хватает гипотенузы
l₂² = (144/5)² + (144/35)²
l₂² = 144²*(1/5² + 1/35²) = 144²*(7²/35² + 1/35²) = 144²*50/35² = 144²*2/7²
l₂ = 144√2/7
Расстояние между вершиной прямого угла исходного треугольника и центром вписанной окружности (r=12)
l₁² = r² + r²
l₁² = 2r²
l₁² = 2*12²
l₁ = 12√2
Коэффициент подобия малого и большого синего треугольников
k = l₁/l₂ = 12√2/(144√2/7) = 7/12
и из подобия короткий катет малого синего треугольника
k = z₁/z₂
7/12 = z₁/(144/35)
z₁ = 12/5