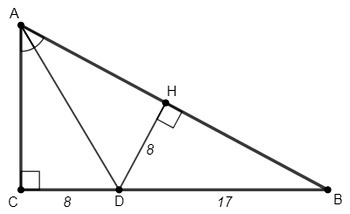
BD=17, DC=8, BC=25
DH - высота на AB
Биссектриса - геометрическое место точек, равноудаленных от сторон угла. Точка D лежит на биссектрисе, DH=DC=8
BH=√(BD^2-DH^2) =√(17^2-8^2) =√(9*25) =15
△ABC~△DBH (по двум углам)
k=BC/BH =25/15 =5/3
S(DBH)=BH*DH/2 =15*8/2 =60
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
S(ABC)=S(DBH)*k^2 =60*25/9 =500/3 (см) ~166,67 см
ИЛИ
Треугольники ADH и ADC равны по острому углу и гипотенузе.
DH=DC=8, AH=AC
Из треугольника DBH по теореме Пифагора находим BH=15
AB =AH+BH =AC+15
AC^2 +BC^2 =AB^2 <=>
AC^2 +25^2 =(AC+15)^2 <=>
AC^2 +25^2 =AC^2 + 30AC +15^2 <=>
AC= (25^2-15^2)/30 = 10*40/30 =40/3
S(ABC)=AC*BC/2 =40*25/3*2 =500/3 (см)